巖礦破碎的強度理論 目錄導航：剪切破壞強度理論   脆斷破壞的強度理論   裂紋擴展理論

巖礦是一種多元力學結構的復雜體系，要從理論上弄清它的破壞原因是十分困難的。現(xiàn)代固體力學也無法指導巖礦的實際破碎工程計算。因此，巖礦的破碎只有采用力學強度理論來解決實際問題。這就是說，既然力學在理論上說不清巖礦為什么會破壞， 就干脆避開巖礦為什么會破壞的問題，而以某種力的狀態(tài)作為破碎的終極原因，釆用直接測量的辦法，測量巖礦斷裂的條件。但是，實際的測量也總是有限的，在最簡單的情況下是采用單位斷裂面積上受力的極限——極限強度來表示斷裂條件。巖礦的極限強度是通過實際測量的途擇得到的。然而，巖礦的應力形式又不是單一的，有時是多種形式的應力同時存在，而且每種應力下巖礦破壞的極限強度是不相同的。那么，在多種應力或組合中，究竟是哪一種應力、應變的極限狀態(tài)或其組合導致破碎的發(fā)生？不同的研究者認識不同，觀察研究的角度不同，因而就有不同的結論，于是，出現(xiàn)了不同的巖礦破碎的強度理論。下面介紹幾種常見的巖礦破碎的強度理論。

(1)剪切破壞強度理論

剪切破壞強度理論認為，物體中只要剪應力增長到某個極限，物體就要產生大的塑性變形而屈服、滑 移或破壞。這種理論甚至認為，一切破壞都是由剪切造成的。屬 于這一理論的有最大剪應力理論、內摩擦理論、八面體剪應力理 論等。按最大剪應力理論，當存在三個主應力且σ₁＞＞σ₂＞σ₃，并以壓應力為正，由力學分析知道其最大剪應力τ_m為：

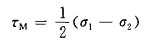
式中σ₁及σ₂分別為最大和最小主應力。當

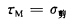
時，物體也就發(fā)生破壞。

固體的破壞理論中，剪切破壞強度理論是研究得比較多的，但此類破壞適用于金屬等塑性材料的破壞，而不適于巖礦材料的破壞。巖礦材料一般硬而脆，幾乎沒有塑性。大多數(shù)巖礦也是不可 壓縮的，其體積壓縮率的數(shù)量級約為10^-6或10^-7,即增加 101. 325kPa時巖礦的體積比較其原始體積減小百萬分之幾或千萬分之幾。對巖礦來說，往往屈服也就破碎了。而且，按最大剪應力理論推論，材料的單向抗拉強度和抗壓強度相等，這個結論對于巖礦是差得太遠了，巖礦的抗拉強度小于抗壓強度的十分之一左右。因此，剪切破壞強度理論對于巖礦材料的破壞是不合適的。

(2)脆斷破壞的強度理論

此理論認為，在三個主應力全是拉伸的情況下，以其中最大拉應力（σ₃）是否達到某一臨界值來作為判斷物體破壞的依據(jù)，而對其余兩個拉應力則不考慮；在拉應 力和壓應力共同作用的情況下，則以最大拉伸應變達到某個限度 作為物體是否發(fā)生斷裂的依據(jù)，而這個限度可以通過試驗確定。最大拉伸應變ε₃為:

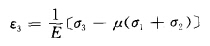
式中           E——彈性模量；

      μ——泊桑比；

σ₁、σ₂、σ₃——三個主應力。

對脆性大的礦物而言，ε₃值不大，韌性大的礦物ε₃較大，即脆性礦物比韌性礦物易破碎。

按照此最大拉伸變形理論必然推得關系：

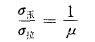
此式中的泊桑比μ值平常在0.2~0.5范圍，故脆斷的抗壓強度是 抗拉強度的2~5倍。但對巖礦來說，此數(shù)值顯著小于實際數(shù)值, 這也許是由于實際巖礦材料中隱藏著裂隙或脆弱面的緣故。與前面的剪切破壞強度理論相比，脆斷破壞強度理論對巖礦材料要更適合一些。

(3)裂紋擴展理論

裂紋擴展理論是由A.格里菲斯于1921年提出來的。他提出這一理論是基于破碎玻璃實際耗費的能量只有理論數(shù)值的三萬分之一這樣一個事實。他做的實驗證明，脆性材料中由于內部存在細微的裂紋缺陷，抗拉強度將大幅度地降低。他提出的假說認為，試件內存在微裂縫，而裂縫尖端有高度的應力集中，以致使裂縫擴展并造成破壞。格里菲斯提出計算臨界載荷的公式為：

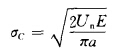
式中         Un——表面能；

            E——彈性模量；

            α——裂縫之半的寬度。

裂縫擴展理論比較適合巖礦材料的破壞，因為巖礦材料既隱藏有缺陷，又具有脆斷的待性，破壞過程有裂縫產生和擴展。

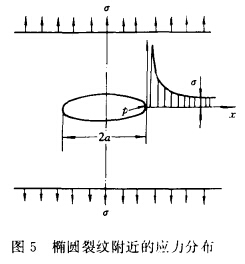
圖5表示一個橢圓裂紋附近的應力分布情況。從圖可見，在離孔遠處，應力分布受孔的干擾很小，基本上是均勻分布的。在長軸的兩端點上，有高度應力集中，而在短軸兩側，應力被卸除，形成低壓區(qū)。當橢圓的短軸長度衰減至零時，便是一條長度為2α√σπ的裂紋。當ρ≤α時，最大應力為：

形成低壓區(qū)。當橢圓的短軸長度衰減至零時，便是一條長度為2α的裂紋。當ρ≤α時，最大應力為：

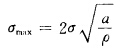
而裂紋附近的各種應力及位移都和Yσ√πα有關，Y是和裂紋方向、型式、尺寸、位置有關的一個系數(shù)。用符號K來表示Yσ√πα稱為應力強度因子。Y值可由專門的分析得到，在手冊中可以查到。

當載荷σ或裂紋長度α達到某一臨界數(shù)值，正好足以使裂紋 發(fā)生擴展，在這種臨界狀態(tài)下的應力場強度因子就稱為斷裂韌性 Kc,它是有裂紋材料斷裂難易的一個判據(jù)。裂紋尖端附近的應力 場強度因子Kc達到什么程度時裂紋才會擴展？單憑力學是冋答不了這個問題的，和前面的力學強度理論一樣，必須通過實際測定才能給出斷裂韌性的數(shù)值來。

這里必須強調指出，巖礦材料由于自身力學性質的特殊性，它的破壞與材料力學中的梁、軸、柱等的破壞有著本質的區(qū)別，故用材料力學中拉、壓、剪應力極限作破碎判據(jù)就顯得不完善。材料力學中研究的各種材料，其抗壓、抗拉、抗剪和抗彎的極限強 度對某種材料而言幾乎是個常量，即每種材料均有自己的材料常 量。但巖礦則不同，不同礦體中產出的同種礦石，或同一礦體中 不同部位產出的礦石，其力學強度均不相同，很難確定巖礦的力 學性質常量，即使同種礦石的某種極限強度測定量值波動范圍也 很大。這就使巖礦的破碎判據(jù)很難確定，即使是前述的三個強度理論，仍然不成熟和不完善，只有借助于試驗測量來確定巖礦的 極限強度。盡管如此，三個破壞的強度理論均明確指出，巖礦的破壞是由于礦塊某種應力超過極限強度所引起的，而且，三個理論也為深入研究巖礦的破碎問題提供了有價值意見。

上述的研究現(xiàn)狀表明，當要對巖礦的破碎作精確的工程計算時，如要計算球磨機中不同礦塊破碎所需的精確破晬力時，靠力學計算是無法解決問題的，也無可靠的巖礦力學常量可供使用，最科學的辦法是按破碎工程的需要進行實際測量。由于各選廠處理的礦石力學性質不一樣，若要計算所需的精確破碎力，只有對該廠礦石進行實際測量。只有這樣才能精確選擇鋼球尺寸。