粉碎過程耗能很多，所以過去對粉碎過程的研究主要是研究功耗問題。現在這方面的研究已取得較多進展。然而，單純功耗理論不是全部粉碎理論，功耗—粒反函數亦不適于描述整個粉砰過程。因而有必要研究粉碎設備的給料和排料之間的關系。

由圖1-9可知，粒度分布的變化是不連續的，而是具有若干峰形曲線的多組成分布。要研究第1組成的粒子是如何進入第2、第3或第n組成的，即要確定各組成間的移動速度，也就是用解析的方法確定速度常數。這是模似化學反應的考慮方法。

胡基、謝得拉切克和巴斯提出了下列聯立方程式

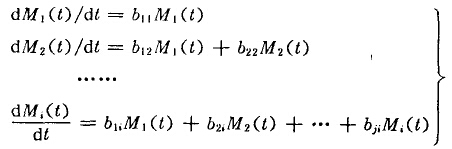
式中M(t)為粉磨t時間后粒度x的篩下量，b(i≠j)表示第j組成的粒子粉碎后進入第i組成移動的質量比例人表示第i組成的粒子粉碎后原粒子的殘留比例；b表示第i組成粒子粉碎成比第i組成小的粒子的移動比例。

方程織(1—43)的解如用行列式表示時，則粒應分布等可用矢量表示，而顆粒各粒度組成間的移動速度可用矩陣表示。

這是將粉碎速度論和粉碎產物粒度分布聯系起來的有效方法。布勞得本特和卡爾考特于1956年提出了如下的粉碎過程的矩陣表示法。

卡爾考持以任意幾何間隔單位。(如篩比)來劃分粒度組成，并把1-a。a-a²，a²-a³，…各間隔的頻率看作列矢量，給料粒度的分布式定義為

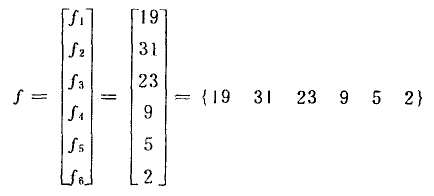
為了研究方便，利用上述表示方法，設粒度分布矢量f＝｛30  20  10｝，并設實際粉碎中正好有一半粒子受到粉碎，即｛15  10  5｝受到了粉碎作用。由表1—9可知，該表最下面總計欄內為粉碎前的粒度分布矢量。經過粉碎后，各粒級的顆粒向更小的粒級變移，其變移的比例(百分數)表示在縱列欄內。例如在開始時處于1-a之間的顆粒，經粉碎后在1-a間隔內殘留6，轉移到a-a²間隔的為3，a²-a³間隔的為3，而其余的(3)則轉入比a³更小的間隔。其次，原來處于a²-a³間隔的顆粒經粉碎后在a-a²間隔殘留4，轉移到a²-a³間隔的為2，轉移到比a³更小間隙的為(4)。各粒度相互之間的變化對最初的｛15  10  5｝的比例可表示如下

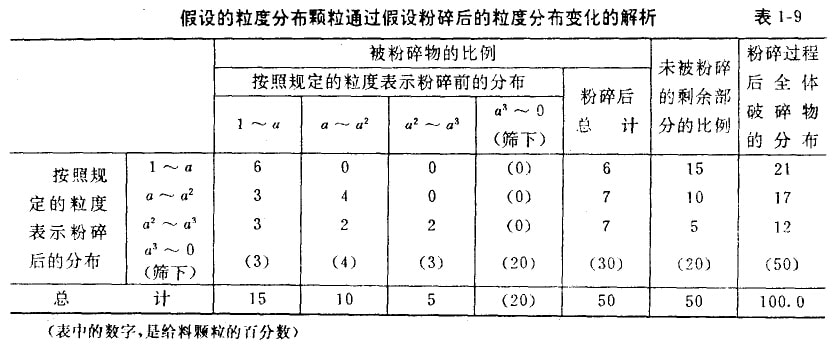
此矩陣表示了粉碎前后各組成粒子的移動狀態，即表示了粉碎特性，故將其定義為碎裂矩陣B，或稱碎裂函數。卡爾考特假定B為如下階梯矩陣

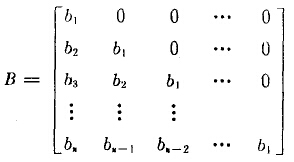
由表1—9可見，粉碎后總計欄表示受粉碎作用的粒子粉碎后的分布。如加上未受粉碎作用的部分，則可得最后一列所示的粉碎后全部粒子的分布，即粉碎作用產生了｛30  20  10｝—｛21  17  12｝粒度分布的變化。

如將這一過程用矩陣表示則可寫成下式

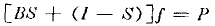
式中P為初碎產物的粒度分布列矩陣，I為單位矩陣，S為選擇函數。

進入粉碎過程的各個粒級受到的碎裂見有隨機性質，即有的顆粒受破裂多些，有的少些，有的則直接進入產品而不受破裂，這就是所謂選擇性或稱概率性。用S表示受到粉碎作用顆粒的比例，即粉碎概率，稱為選擇函數，并假定為對角陣

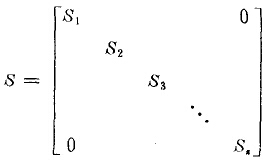
在本例中S=0.5。

本例P的計算如下

上述是一次粉碎的情況。矩陣模型是把粉碎過程看作一系列川繼發生的粉碎事件，后一次的給料是前一次的產品，對于二次反復粉碎則為

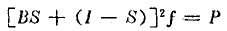
因而在進行n此反復粉碎后，則成為

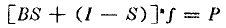
由于缺少提供關于物料固有碎裂特性的非破壞性試驗方法，所以碎裂函數B是一個很難用實驗方法確定的兩數。但是，在給定設備中粉碎特定物料時，存在一種持有的產品粒度分布形式，它和被碎料的性質和對其施加作用力的條件有關。布勞得本持和卡爾考特于1956年建議采用羅辛—拉姆勒方程的修正式表示，即

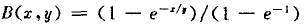
式中B(x，y)，表示原來粒度為y經粉碎后小于x粒徑的質量分數。因而有的學者把破裂函數B又稱為分布函數。

對于選擇函數S來說，與粉碎機械的粉碎機理、碎料的性質和粒徑等有關。但是至今還沒有理論解，只是用實驗的方法在特定粒度范圍內有如下的關系

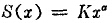
式中x為粒徑，K和α為常數。